実験結果
本実験結果と先行研究結果
| 弾丸の種類 | 衝突速度(km/s) | マイクロスコープを用いたクレーター体積(cm3) | クレーター深さ(mm) | 横方向クレーター径(mm) | 縦方向クレーター径(mm) | 円錐仮定のクレーター体積(cm3) | 標的密度(g/cm3) |
|---|---|---|---|---|---|---|---|
| ナイロンvs砂岩 | 6.875 | 0.126025 | 12.067 | 9.3530 | 9.4980 | 0.2806409 | 2.5 |
| WCvs砂岩 | 2.047 | 0.642861 | 17.299 | 9.1570 | 10.714 | 0.4443185 | 2.5 |
| アルミナvs砂岩 | 3.779 | 0.607882 | 12.355 | 11.688 | 10.814 | 0.4088254 | 2.5 |
| ガラスvs砂岩 | 4.794 | 0.127166 | 12.054 | 9.1950 | 10.068 | 0.2921425 | 2.5 | ナイロンφ3mm vs砂岩 | 6.814 | 0.655677 | 15.140 | 28.745 | 30.614 | 3.4880033 | 2.5 | チタンvs砂岩 | 3.046 | 0.163415 | 12.226 | 11.299 | 9.8360 | 0.3557226 | 2.5 |
| 弾丸の種類 | 弾丸径φ(mm) | 質量(mg) | 密度(g/cm3) | 衝突速度(km/s) | クレーター体積(cm3) | 標的密度(g/cm3) |
|---|---|---|---|---|---|---|
| ナイロンvs砂岩 | 7 | 219.157 | 1.22029 | 3.90 | 9.3675 | 2.6 |
| ナイロンvs泥岩 | 7 | 219.157 | 1.22029 | 4.37 | 31.854 | 3.1 |
| ナイロンvs大理石 | 7 | 219.157 | 1.22029 | 3.85 | 7.7387 | 2.7 |
| ナイロンvs中国砂岩 | 7 | 219.157 | 1.22029 | 4.21 | 3.9658 | 2.2 | ナイロンvs大理石 | 7 | 219.157 | 1.22029 | 4.20 | 17.796 | 2.7 | ナイロンvs砂岩 | 7 | 219.157 | 1.22029 | 4.20 | 1.4900 | 2.6 | ナイロンvs大理石 | 7 | 219.157 | 1.22029 | 2.31 | 4.2557 | 2.7 | ナイロンvs泥岩 | 7 | 219.157 | 1.22029 | 1.91 | 1.6395 | 3.1 | ナイロンvs中国砂岩 | 7 | 219.157 | 1.22029 | 2.22 | 6.1528 | 2.2 | ナイロンvs砂岩 | 7 | 219.157 | 1.22029 | 3.90 | 7.7213 | 2.6 | ナイロンvs中国砂岩 | 7 | 219.157 | 1.22029 | 3.96 | 11.155 | 2.2 | ポリカーボネートvs砂岩 | 14.8 | 4335.247 | 1.26 | 0.8197 | 11.274 | 2.5 |
| ポリカーボネートvs砂岩 | 14.8 | 4335.247 | 1.26 | 1.035 | 67.540 | 2.5 |
| ポリカーボネートvs砂岩 | 14.8 | 4335.247 | 1.26 | 0.832 | 13.385 | 2.5 |
| ポリカーボネートvs砂岩 | 14.8 | 4335.247 | 1.26 | 0.996 | 18.143 | 2.5 |
スケーリング則の式を下記に示す。
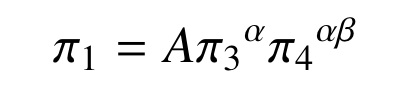
今回の実験ではπ3を一定にすることにより、π1とπ4の関係からAとβを求める。そして求めたβから、これまで行ってきた一連の実験のデータを組み合わせることでαを求め比較する。
第1段階:今回の計測データの値を用い、αβを求める。
第2段階:全データを用いαを求め、第1段階で求めたαβを用いβを求める。
解析結果
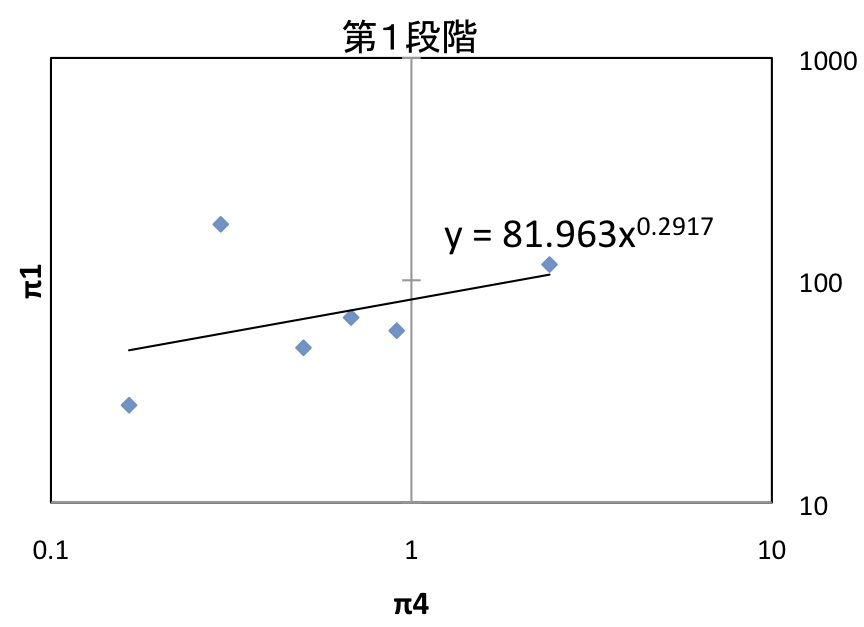
図9:第1段階
第1段階よりαが求まる。
αβ=-0.2917
次に第2段階の計算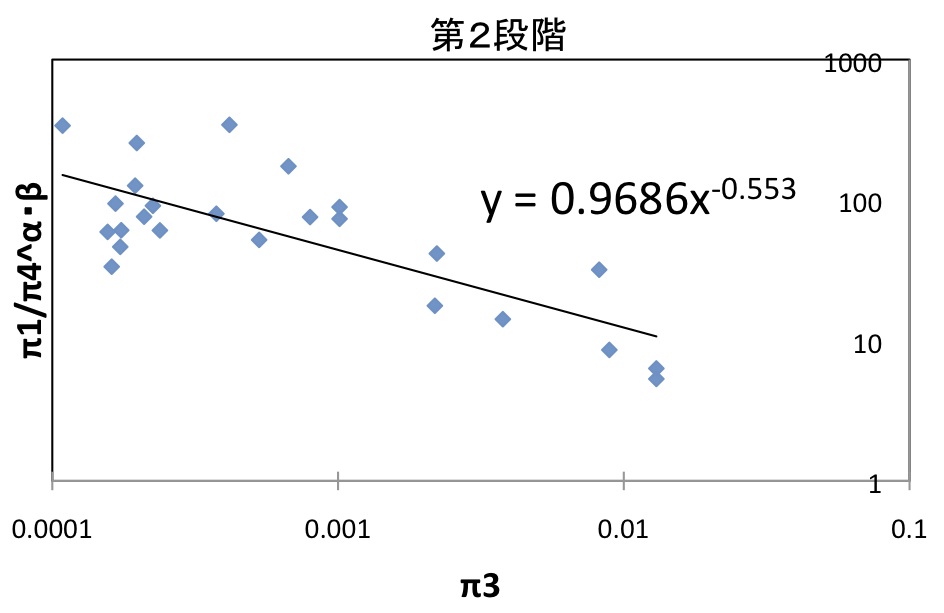
図10:第2段階
α=-0.553 , β=-0.527 , A=0.969
考察
(1) 金属を使ったスケーリング則との比較
先行研究より金属スケーリング則の値は求まっている。.jpg)
図11:Holsapple_and_Schmidt(1982)
α=-0.709 , β=-0.738 , A=0.458
この値と今回求めたαβを比較するとαβ_[金属]=0.523 > αβ_[堆積岩]=0.291
グラフにしたのが下図になる。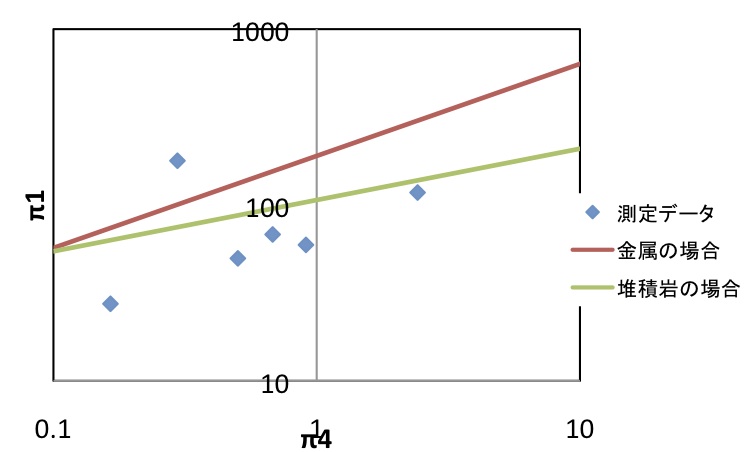
図12:金属スケーリング則との比較
→堆積岩の方がターゲットと弾丸の密度比の変化によるクレーターの大きさの変化が小さい。
→今回の実験で求めたαβを使うことで、実際に惑星表面で隕石が衝突した場合の隕石と衝突地点の 密度比の推測の誤差を小さくすることができる。
同様にαを比較すると
α_[金属]=-0.709 < α_[堆積岩]=-0.553
グラフにしたのが下図になる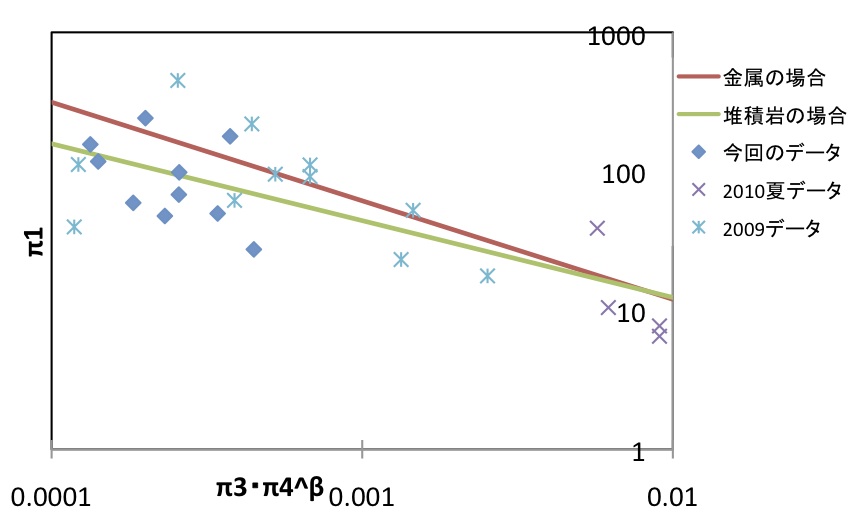
図13:金属スケーリング則との比較2
→堆積岩の方がターゲットと弾丸のπ3の変化によるクレーターの大きさの変化が小さい。
→今回の実験で求めたαを使うことで実際に惑星表面に隕石が衝突した場合のπ3の推測の誤差を 小さくすることができる。
(2) 体積に関する考察
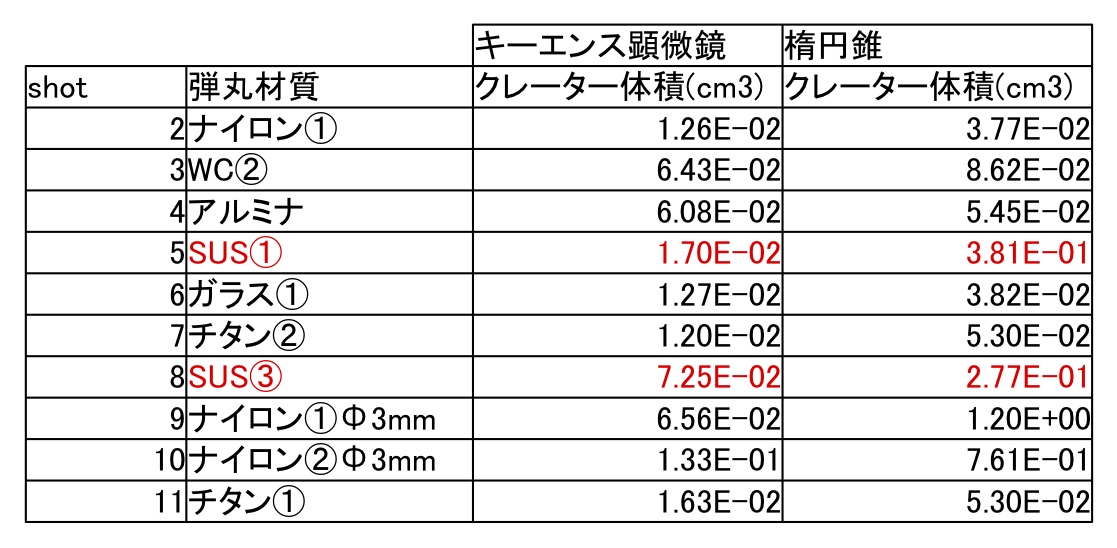
上表によると顕微鏡と楕円錐近似の体積測定の違いは、SUSの場合顕著になる。これは、SUSによるクレーターのスポレーションが不完全であったことが原因とされる。そこで、SUSの体積のみをスポレーションしていない径で同じ評価をすると、
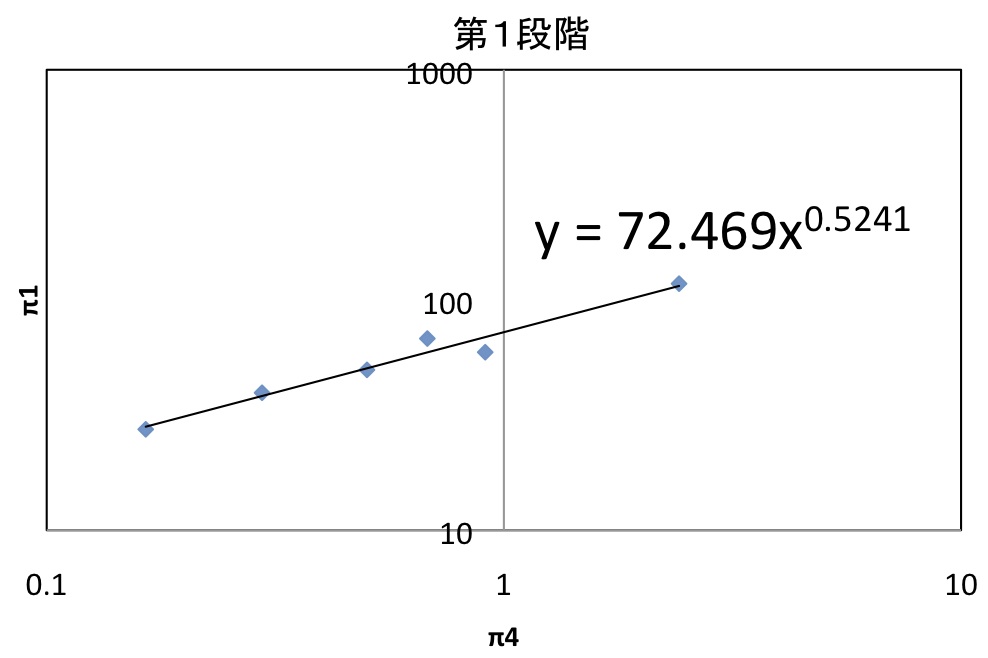
図14:体積補正した第1段階
αβ=0.5241
全データよりαを求めると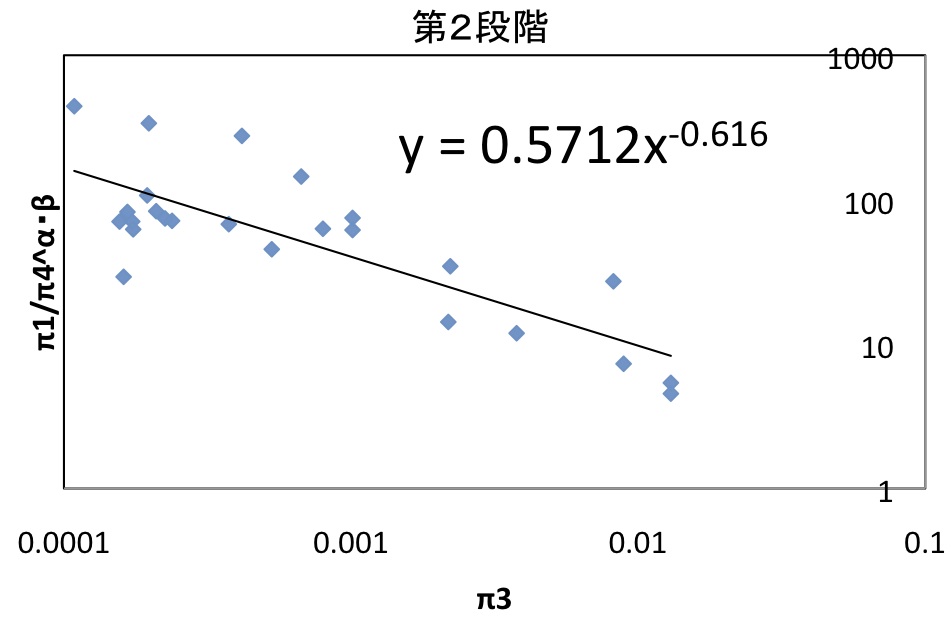
図15:体積補正した第2段階
α=-0.616 , β=−0.851 , A=0.571
これを金属スケーリングと比較すると、α_[金属]=-0.709 < α_[堆積岩]=-0.616
β_[金属]=-0.738 > β_[堆積岩]=-0.851
αβ_[金属]=0.523 = αβ_[堆積岩]=0.524
堆積岩と金属を比較してみると、αβほぼ同じ値だがαが異なるためβも金属と堆積岩で値が異なる。 このことから、スケーリング則を下記の表記にすることを提案する。そうすることでターゲットが金属であっても堆積岩であってもπ4の乗数を同じとすることができる。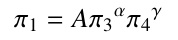
今後の課題

図16:クレーターの違い

図17:弾丸強度とクレーターの違い
ナイロン→スポレーションを起こさない
SUS→スポレーション起こしかけ
WC→弾丸による掘削
これらの違いは、スケーリング則に弾丸強度が関係を示唆している。 すなわち、
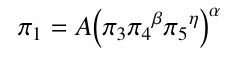
上式のように、弾丸強度の項をスケーリング則に組み込む必要がある。
Last modified: 11.01.12
Copyright © 2009-2010 Impact Research Group. All rights reserved.
Copyright © 2009-2010 Impact Research Group. All rights reserved.